Решения задач обсуждаются коллективно, анализируются различные способы решения, проводится обобщение полученных результатов, формулируется учебная проблема и намечается способ ее решения. Всячески поощряется самостоятельность суждений, отстаивание учащимися собственного мнения. (Смотри приложение 2)

Идея использования вспомогательных задач возникла на основе наблюдений психологов о том, что при решении сложной задачи учащиеся обычно ищут, под какой из уже известных типов задач можно было бы ее подвести. При этом они, анализируя условие задачи, осуществляя поисковые пробы, пытались вос­пользоваться такими данными, которые способствовали бы пере­носу уже имеющегося в их опыте (полученном при решении ранее встречающихся задач) общего или частного метода, способа или приема решения задач. То есть способы решения одной задачи оказывают существенное влияние на самостоятельные поиски решения другой.

Вспомогательные задачи являются своеобразными указания­ми к самостоятельной деятельности ученика при решении основ­ной задачи. Они отличаются от указаний и готовых решений, имеющихся в большинстве пособий по математике для самостоя­тельной подготовки к конкурсным экзаменам, тем, что не содер­жат рецептов, не навязывают способ решения автора, не дают готового решения. Указание (подсказка) во вспомогательной задаче заключается в ее решении: нужно сначала самостоятельно решить вспомогательную задачу, а затем обнаружить содержа­щуюся в ней подсказку. Обычно для ученика одной вспомога­тельной задачи оказывается недостаточно. Тогда дается вторая вспомогательная задача и т. п. Образуется серия вспомогатель­ных задач.

Схематично основная задача А вместе с серией вспомога­тельных задач A1, A2, ., An изображается так: А: A1 —A2 — . —An.

Самостоятельная деятельность ученика начинается с решения задачи А. Если он за определенное время не сможет решить ее, то приступает к решению первой вспомогательной задачи А1: А—А1. В случае решения задачи А1 ученик снова возвраща­ется к задаче А: А1—А. Если задача А снова не решается, то он обращается к задаче А2. Решив задачу A2, возвращается к зада­че A и т. д. Возможен случай, когда школьник не сможет решить вспомогательную задачу А1. Тогда он приступает к решению задачи А2. Если и A2 не решается, то переходит к задаче A3 и так до An. От задачи An ученик последовательно возвращается к задаче

А: An —An-1 — . —A1—A. Возможна и другая последо­вательность решения задач, что можно изобразить схемами:

A —A1 — A—A2 —A — A3 —A или

A —A1 — A—A2 —A1 — A—A3 —A2 —A1—A и т. д.

Составление вспомогательных задач наталкивается на серьез­ные трудности. Для решения задачи Л может соответствовать и другая серия вспомогательных задач, отличная от указанной, например В1, В2, ., Bk Трудность заключается в отборе лучшей (оптимальной) серии для конкретного ученика. Далее, серия может быть и нелинейна. Это получается тогда, когда для реше­ния задачи A нужно знать способы решения сразу двух (или нескольких) задач. Схематическое изображение этой ситуации таково:

A: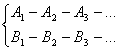

Трудность заключается в том, что одна и та же серия вспомо­гательных задач для разных учащихся имеет различную эффек­тивность: для одних серия слишком длинна (содержит много задач), для других коротка, одни и те же задачи для одних слишком легки, для других трудны и т. п. Кроме того, вспомо­гательные задачи навязывают ученику определенный путь реше­ния. Но и при подсказке учителя также навязывается ученику способ решения, намеченный учителем.