Приведем примеры.

1. В IX классе на занятии математического кружка было предложено найти способ (путь) решения задачи: «Найти уравне­ние прямой, параллельной прямой у=2х—3 и проходящей через точку К(—3; 2).

Известная из аналитической геометрии формула у—у0=k(х—х0) учащимся не сообщалась. Они самостоятельно должны были отыскать путь решения предложенной задачи.

Решение.

Способ 1. Ученик предложил на прямой у=2х—3 рассмотреть любую точку, например А (0; —3). Затем в формулах параллель­ного переноса х'=х+а, у'=у+b подобрать параметры а и b так, чтобы точка A перешла в точку К. Это будет перенос: х'=х—3, у'=у+5. Прямую у=2х—3 подвергнем найденному параллель­ному переносу: x = x'+3; y = у'— 5;

у'— 5=2 (x'+ 3)—3; у'—5= 2x'+6—3; y'==2x'+8. После отбрасывания штрихов при пе­ременных получим ответ: y =2x+8.

Способ 2. Ученик предложил воспользоваться известным фактом, что в уравнениях параллельных прямых угловые коэф­фициенты равны. Поэтому искомое уравнение будет вида у=2х+b. Последнему удовлетворяют координаты точки K, по­этому 2=2×(-3)+b, b=8.

Ответ: y==2x+8.

2. В стенгазете математического кружка IX класса было предложено самостоятельно найти способы решения задачи: «Вы­числить расстояние от точки M (3; 2) до прямой Зх+4y+1=0».

Ученики нашли различные способы решения.

Способ 1. Воспользоваться готовой формулой, найденной учеником в учебнике по аналитической геометрии для втузов:

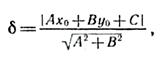
где Ах+Ву+С=0 — уравнение прямой, a x0 и у0 — координаты заданной точки.

Способ 2. На прямой Зх - 4y + 1 = 0 способом подбора найти две точки, например A (1; 1) и В (—3; —2). В треугольнике АВМ вычислить длины сторон и по формуле Герона площадь. Затем найти высоту, проведенную к стороне АВ. Это и будет искомое расстояние.

Способ 3. Найти уравнение прямой, проходящей через точку М перпендикулярно данной прямой. Затем вычислить координаты х0 и у0 точки пересечения этих прямых. Расстояние от точки (3; 2) до точки

(x0; у0) и будет искомым.